在阅读此文前，麻烦您点击一下“关注”，既方便您进行讨论与分享，又给您带来不一样的参与感，深度长文，希望您能够认真看完，感谢您的支持!

人类是地球上最有智慧的生命，和其它动物最大的区别在于，人类依靠自己的智慧，站到了地球食物链的顶端，这说明人类科技发展的速度很快，人类之所以能够有如此之快的发展速度，离不开科学家的贡献，而数学对于科学发展来说也是至关重要的，数学是科学研究的基础语言和工具，在物理学中，牛顿用微积分来描述物体的运动和万有引力定律，爱因斯坦通过复杂的张量分析建立了广义相对论。在化学里，数学用于计算化学反应的速率、物质的结构等。在生物学中，数学模型可用于研究种群增长、基因遗传等。通俗一点来说，所有的自然科学领域都离不开数学。

而且数学在推动技术进步方面有很大的成效，从计算机的发明到现在的人工智能，都是以数学为核心支撑，算法设计基于数学原理，数据加密依赖于数论中的复杂算法，数学为技术创新提供了理论依据和方法，能够让科技不断突破，改变着人们的生活方式和社会发展进程，数学的发展是一个漫长而复杂的过程，最早能够追溯到公元前600多年前，泰勒斯被称为是数学的鼻祖，他是第一位将数学从经验提升到理论层次的哲学家，提出“万物皆数”的哲学观点，并且证明“圆周角定理”“对顶角相等”等命题，开创几何证明传统。在公元前500年左右，毕达哥拉斯创建学派，强调数学和哲学的结合。

发现了勾股定理，推动了几何学的发展，不过根据记载，当时我国的数学也是非常发达的，据《周髀算经》记载，提出“勾三股四弦五”的勾股定理特例，早于毕达哥拉斯学派500年。到了公元前200多年，阿基米德发现了杠杆原理，将数学应用于力学研究，后来到了17世纪中叶，杰出的数学家越来越多，欧几里德（古希腊，约公元前330年-前275年）著《几何原本》，以公理化体系（5条公设+5条公理）构建几何学，成为2000多年西方数学教育的基石。刘徽（中国，魏晋时期，约公元3世纪） 发明“割圆术”，用极限思想计算圆周率（π≈3.1416），推动中国数学的算法化。

之后到了19世纪-20世纪的时候，笛卡尔、牛顿、莱布尼茨、欧拉、高斯、黎曼等众多数学家崛起，让人类的科技发展越来越快，到现在为止，数学依然是人类探索的方向，因为数学还没有被人类解开，数学的奥秘远远超过人类的想象，数学世界中最朴素的事物是素数，人类从未真正的理解过它，它定义简单——不能被更小的整数整除，却构成了整个自然数的乘法根基，每一个数都是素数的积，且拆解方式是唯一的，这一事实，欧几里得在2000多年前就说清楚了，素数，又称质数，是指在大于1的自然数中，除了1和它自身外，不能被其他自然数整除的数。例如，2、3、5、7、11等都是素数，而4能被2整除，6能被2和3整除，所以它们不是素数。

素数有无穷多个。这一结论最早由古希腊数学家欧几里得在其著作《几何原本》中给出了经典的证明。假设素数是有限个，设为，考虑数。如果是素数，那么它是一个新的素数；如果是合数，那么它必然有一个素因子，而不可能是中的任何一个，否则能整除，这是不可能的，所以素数有无穷多个。随着自然数的增大，素数在自然数中的分布会越来越稀疏，对于素数来说，人类在生活中的应用还是非常多的，素数在现代密码学中起着核心作用。例如，RSA算法利用了两个大素数相乘容易，但分解乘积得到原来的素数却极其困难的特性来实现加密和解密。如果能够快速分解大整数为素数，那么RSA算法就会被破解，但目前还没有有效的算法能在合理时间内完成这一任务。

在哈希函数中，素数常被用于计算哈希值，以减少冲突的概率，提高哈希表的性能。此外，在一些随机数生成算法中，素数也被用来保证生成的随机数序列具有良好的随机性和均匀性。虽然素数在很早的时候就被人类发现了，但为什么会这样？现在科学家也很难解释清楚，这种看似随机的，又不是随机的本质，让科学家们难以理解，素数有着明确的数学定义，这一定义是确切的、非随机的，根据这个定义能够准确的判断一个数是不是素数，并且，素数在整数排列中是客观存在的，而且是固定的，每一个素数都有其特定的位置和数值，并不是随意出现的，例如算术基本定理，它表明任何大于1的自然数都可以唯一分解成若干个素数的乘积。

这体现了素数在数论体系中的基础性和确定性，它们是构建自然数的“基本元素”，其分布和性质受到严格的数学规律制约。再如素数定理，精确地描述了素数在自然数中的大致分布密度，随着自然数的增大，素数的分布越来越稀疏，这是一个可预测、有规律的趋势。但为什么说它像极了随机？尽管有素数定理描述素数的整体分布趋势，但是具体到每一个素数的出现位置，却没有明显的规律可言，例如，2和3是相邻素数，它们的间隔为1；而7和11是相邻素数，间隔为4；在更大的数中，相邻素数的间隔可能更大且变化无常。这种间隔的不确定性使得素数的分布看似随机，难以准确预测下一个素数会在何处出现。

从统计学的角度来说，素数在某些方面有类似随机序列的性质，比如说在一个给定的区间内，素数的个数大致符合某种统计规律，但是具体有哪些数是素数却像是随机选择的，素数不是随机的，是因为它们有严格的定义和内在的数学规律；而它们又像极了随机，是由于其在分布、余数等方面表现出的不规则性和类似随机的统计特性。这种独特的性质使得素数在数学研究中具有重要的地位，也吸引着数学家们不断深入探索其中的奥秘。素数其实只是数学当中，一个分支而已，整个数学的魅力是人类至今都无法解释的。数学就像是一条没有尽头的长河，永远都不可能找到它的边界。

在巴黎蓬皮杜艺术中心的数学展厅里，当参观者通过触摸屏重构黎曼猜想的三维模型时，那些跃动的几何线条仿佛正编织着宇宙的源代码。这个场景恰如其分地揭示了数学的本质：它既不是冰冷的符号游戏，也不是单纯的实用工具，而是一场永不停歇的人类思维远征。在这场远征中，数学以其特有的方式，不断突破认知边界，展现出令人着迷的无限可能。自然数的无穷序列构成了数学大厦的基石，这个看上去简单的概念却蕴含着深刻的哲学意蕴，古希腊哲学家亚里士多德曾经说过“无限只是潜在的”，但是数学家却在实数轴上构建起了完整的无限体系。

数学发展了几千年，有很多现在人类都无法解开的难题：

1、科拉兹猜想：对于每一个正整数，如果它是奇数，则对它乘3再加1，如果它是偶数，则对它除以2，如此循环，最终都能够得到1。虽然目前通过计算机验证了大量的数字都符合这个猜想，但尚未能从理论上证明对于所有的正整数都成立。

2、哥德巴赫猜想：任何一个大于2的偶数，都能够表示成两个素数之和，目前最好的结果是中国数学家陈景润在1973年发表的陈氏定理，证明了任何一个充分大的偶数都能够表示成两个素数和一个素数以及一个半素数的和，但是距离完全证明哥德巴赫猜测还差的很远。

3、孪生素数猜想：存在无穷多个素数p，使得p + 2是素数，素数对(p, p + 2)称为孪生素数。2013年美籍华裔数学家张益唐证明存在无穷多个素数对相差都小于7000万，之后数学家们不断降低这个差值，但最终要证明素数对相差为2，可能还需要很长时间。

4、黎曼猜想：在1859年的时候，黎曼提出所有非平凡零点都位于复平面上实数部分为二分之一的直线上，简单来说，若s是一个非平凡零点，则s的实部必须等于二分之一，如果说黎曼猜想能够成立，将会帮助数学家更加清晰的理解素数出现的规律，尽管经过了多次计算机的验证，黎曼猜想依然没有得到严格的证明和反证。

5、接吻数问题：当一堆球体堆积在某个区域中时，每个球体都有一个“接吻数”，即它所接触的其他球体的数量。对于1维、2维、3维空间，接吻数问题已得到解决，但超过3个维度，接吻数问题大部分尚未解决，数学家仅将可能性缩小到了多达24个维度的相当窄的范围。

6、大基数问题：在集合论的数学领域中，大基数性质是有限基数的一种性质。数学家不断发现越来越大的基数，虽然一些定理对大基数的可能性施加了某种限制，但仍存在许多悬而未决的问题。

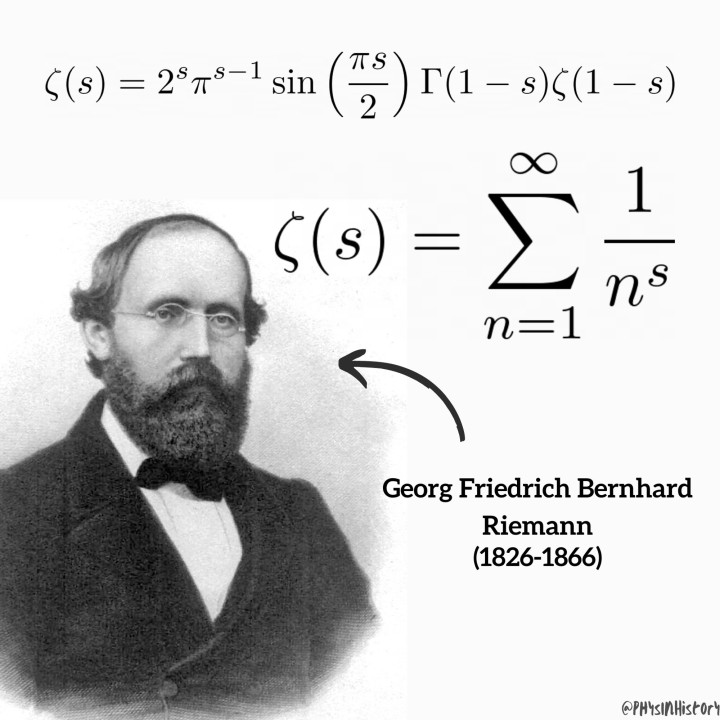
除了这些数学上人类无法解释的奥秘之外，还有很多数学奥秘是现在人类没有办法解开的，而且还有很多人类到现在还没有发现的数学奥秘，数学到底有多么神秘，可能只有创造它的人才懂，数学中隐藏着无数看似巧合却又蕴含深刻规律的现象，而且在数学中，很多概念已经超越了我们日常的直观感受，比如说高维空间、无穷集合等，数学经常能够预测一些还没有被发现的现象或者事物，在物理学中，很多理论都是通过数学和公式推导出来的，之后才在实验中得到了验证，数学中有很多新的问题，旧的问题解决了，就会出现很多新的问题。数学的领域不断拓展，从传统的代数、几何、分析到现在的拓扑学、密码学、分形几何等新的领域。

数学的边界在不断的延伸，随着人类认知水平的提高和科技的发展，我们对数学的理解也在不断的深化，如果你仔细发现，就能够感觉出来，我们的宇宙运行，规律、规则等等，好像都是按照数学来设计的，它就像是一个巨大的数字模型一样，包含了我们所能够想到的一切问题和根源，这个巨大的数学模型，是人类现在无法想象的，在我们现在看到的宇宙外面，还可能存在多维的宇宙空间，更高维度的时空等等，这一切的一切都是通过数学来构建的，所以想要解开宇宙的奥秘，就必须解开数学的奥秘。但是对于人类来说，这是非常困难的，未来随着人类科技的进步，说不定人类能够解开更多的数学奥秘，对此，大家有什么想说的吗？